乱流現象の数値実験

大規模計算機システム利用者報告

乱流現象の数値実験

梶島　岳夫（大阪大学大学院工学研究科　機械物理工学専攻）

１．はじめに

　本年度より始まったシェアウェアサービスを、科学研究費補助金特定領域(B)「乱流要素渦による乱流理論・予測・制御の新展開」（平成12.14 年度、代表：核融合科学研究所木田重雄教授）の計画研究D「乱流の予測制御と乱流要素渦」の一員として利用した。計画研究D は三宅裕教授（大阪大学）、宮内敏雄教授（東京工業大学）、笠木伸英教授（東京大学）と筆者から構成され、三宅研究室でシェアウェアグループを登録した。ここでは、筆者の行っている計算について上記の科研以外のテーマも含めて紹介したい。
　科研プロジェクトにおいては、添加物による乱流変調と、変調を受けた乱流の構造の研究を行っている。前者では、具体的には、ポリマー・界面活性剤・ファイバーなどの添加による乱流抵抗の削減効果、固体粒子・液滴・気泡などの分散相による乱流変調の２項目を対象としている。後者では、操作を受けた乱流場の代表例として、圧力勾配による乱れの増加・減少に関与する渦構造の解明のため、徐々に拡大または縮小する流路内の直接数値シミュレーションを実施している。その他、熱流体の数値シミュレーションにおける新たな解法として注目されており、ベクトル並列型計算機に適すると考えられる格子ボルツマン法を乱流に適用する研究も実施している。

２．計算例

２．１固体粒子を含む乱流

固体粒子が乱流渦構造に及ぼす影響を解明するため、モデルをいっさい用いることなく、多数の粒子の周りの流れと流体の乱流をフルスケールで解析する方法を適用して乱流変調を再現することを試みている。SX-4 では粒子分布のパターンを観察できるに止まったが、今年度はSX-5 でスケールアップを図り、粒子群が引き起こす最大スケールの乱れに相当するクラスター間の相互作用までが視野に入ってきた。図1 はその一例で、一様な流れ場を落下する粒子の分布の時間発展を示している。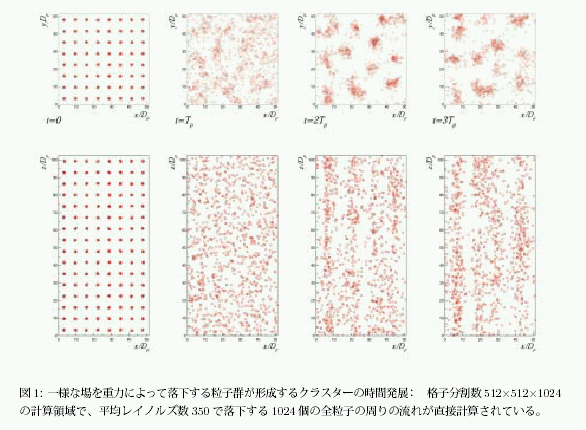

２．１空間的に非平衡な乱流

　乱流は文字通り変動を含んだ流れであるから、計算領域の境界が固体壁面や非乱流域でなければ、全ての境界で乱れも与えなければならない。ところが、流入してくる乱れを空間的かつ時系列でリアルに与えることができるなら、そもそも乱流計算など必要ないのである。現実にはそのような理論は存在しないので、様々の近似的な境界条件が考えられている。前節の例は、各方向に周期条件を与えており、「十分発達した場の一部を切り出した」と解釈される。もちろん、計算領域より大きな現象については周期性という「モデル」である。
　従来の乱流計算は、主として十分に発達した状態を対象としてきた。自然現象や工学的に取り扱われる流れのように、流れ方向に変化する場合は難しい。しかし、最近では空間的に発達する流れ場を扱う方法が検討され、境界条件の工夫だけでなく大規模計算の御利益もあるが、非平衡な場での乱流構造が数値シミュレーションの対象となってきている。そのような例を以下に示す。
加速乱流（図2）　縮小する流路における加速流れでは、乱れが減少し、場合によっては層流化することが知られており、圧力勾配という操作を受けた渦構造の観点から興味深い。そこで、十分に発達した平行平板間流れから、一方の壁にスロープをつけて徐々に縮小させ、加速流れにおける乱流の直接シミュレーションを実施した。図2 に縮小流路における瞬時の渦構造を示す。主流速度が加速されることによって速度変動は相対的に低下するが、低速乱れは長く存続している。しかし、それにまとわりつく渦は徐々に消失しており、生きている（維持されている）乱れと、死んだ乱れの違いがよくわかる。
減速乱流（図3）　拡大する流路は、流体機械で羽根の回転で与えたエネルギーを圧力に変換するデフューザーなどに見られる。その乱流構造を調べるため、流入条件は十分に発達した平行平板間乱流とし、対流流出条件を用いて、計算領域を空間発展型の場とする計算を実施した。流れを駆動させるために、平行平板間乱流を周期境界条件で並行して計算し、その１断面を上記の流入条件に供給した。現状は十分な時間発展が終了した段階であり、これからデータベース化して乱流構造の解析に取りかかるところであるが、拡大比4.7 の場合の瞬時の流れの例を図3 に示す。

２．３格子ボルツマン法による乱流計算

　格子ボルツマン法は、流体が連続体であることを前提としてナビエ・ストークス方程式を差分法・有限体積法・有限要素法などで計算する従来の解法とは異なり、仮想粒子の衝突と平均を繰り返して連続体の流れを模擬しようとする方法である。ある条件で、格子ボルツマン法の方程式がナビエ・ストークス式に帰着することは理論的に示されている。この方法は、非常に複雑な流路形状や、多孔質などの媒体内の流れ、気・液・固の複数の相が混在するの多相流などへの適用性の観点で注目されている。しかし、単相乱流の直接計算では従来の方法に対する優位性はそれほど認められていない。とは言うものの、たとえば円管内の乱流という最も基本的な流れを考えると、円柱座標では中心の特異性の問題、デカルト座標では曲面壁の問題があって、実は従来法による計算はほんの二三例に止まっている。図4は、この課題に対して格子ボルツマン法の適用を検討し、壁面境界条件および格子方向性に関して新たなモデルを開発して得られた計算結果の例である。

３．おわりに

　計算結果をTecplot やFieldview といった可視化ソフトに用いるため、研究室のワークステーションやパソコンに移さなければならない。ネックはそのための転送時間である。たとえば、図1 の例では計算結果をパソコンについているDVD-RAM にセーブしているが、単精度に落としても瞬時の流れ場（速度の3 成分と圧力、および粒子に関するデータ）を学内LAN で転送するのに3 時間近くを要する。図1 に示した例は約31GB のサイズであり、SX-5の1 ノードで十分である。したがって、途中データの入出力なしで約10003 の格子数までは可能である。現在実施されている最大規模の乱流計算は格子数20483 といわれている。阪大のSX-5 の一般利用サービスであればその中間の規模の計算はできる。乱流は本質的に三次元現象だから、スケールアップは3 方向に行う必要があり、それに伴って時間刻み数も増やさなければならない。しかし、各方向に2倍（したがって、計算規模は約10 倍）しても、対数尺で見れば0.3 桁だけスケールが増えるにすぎない。乱流は広範な連続スペクトルをもつ非線形現象であるから、格子数10003 .20003 の大規模計算を行ったところで、扱えるのは3 桁にすぎない。数値シミュレーションで最も重要なことは、その3 桁をどこに設定するかである。その意味では装置の設計で実験の成否が概ね決まることと似ている。その次に、計算されないスケール（赤外側と紫外側）をどのように扱うかというモデルが重要になる。計算のスケールアップは、そのモデルがクリティカルな場合のみ意味がある。そういう訳で、mpi32 やmpi64のクラスも設定されているが、前述のデータ保存時間の問題も考えると、現状以上の大規模計算をする時期ではないと考えており、シェアウェアで16p クラスのジョブを多く流せる環境はわれわれ乱流計算には非常に快適である。
図4: 格子ボルツマン法で求められた円管内乱流：
断面内の乱れ。