業務及び研究の報告

ナノメートルサイズの永久磁石　
－ 常磁性多核錯体のリバイバル－

中野　元裕・松林　玄悦
(大阪大学大学院工学研究科　分子化学専攻)

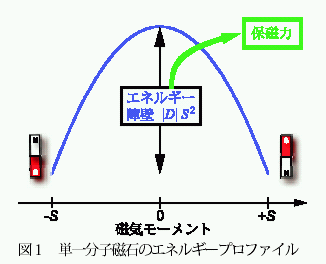
　　最近、錯体化学の分野でリバイバルしているテーマに「常磁性多核錯体の磁性」がある。常磁性多核錯体というのは、複数の遷移金属イオンが配位子で架橋されてひとつの分子になったもののことで、有限個のスピンが強磁性的あるいは反強磁性的に相互作用するモデルで表すことができ、その基本的なエネルギー状態や磁性は'50-60 年代に解明されたというのがこれまでの認識だった。ところが'90 年代もなかばになって、大きな基底スピン（S = 10 など）をもつ多核錯体は予想外なことにかなり古典的な磁石として振る舞う、つまり錯体分子のどこに磁極があるのか決めることができて「単一分子磁石」と呼べるような挙動をとることが明らかとなって、再び盛り上がりを見せている[1, 2]。

　　この単一分子磁石系物質の特徴は、すでに述べた大きな基底スピンをもつことに加えて、分子が容易軸型の大きな磁気異方性を有するという点にある。この異方性が分子の赤道方向に高いエネルギー障壁をつくって分子磁化の反転を妨げ、ナノメートルサイズの永久磁石を実現している（図１）。
さて、この異方性を記述するには通常、一軸性のゼロ磁場分裂パラメーターD をはじめとするスピンハミルトニアン・パラメーターが用いられるのだが、磁化曲線や磁化率、高周波電子常磁性共鳴（HFEPR）などの実験結果からパラメーターを抽出するためには適当なモデルを仮定したフィッティングやシミュレーションが欠かせない。計算内容は、行列の対角化でスピン準位のエネルギー固有値を求め、対応する物理量の統計平均を取るという単純なものだが、スピンが大きいためやややっかいである。

　　ところで、粉末試料においては試料中の分子が磁場に対していろいろな方向をとっているため、等方性の分子の場合を除きランダム配向を仮定して平均操作を行う必要がある。具体的には、分子上に固定した座標系で磁場の方向を極角θ方位角φで表し積分する操作

である。一般的にはサンプリング方向としてレベデフ節点を用いた球面ガウス求積など[3] で計算されるが、分子の異方性が軸対称をもつときには方位角を振る必要がないので１次元のガウス求積[4]を行えばすみ簡単である。磁気共鳴の吸収線型のシミュレーションなどに当たってはサンプリング方向を数千点は欲しいところだが、磁化やエントロピーなど熱力学量の計算では十点程度でもかなり良い近似になる。

　　さて、最近の計算機の進歩は実験屋にとっても強い味方である。ネットワーク上を探せば粉末平均にせよ[3, 4] 対角化にせよ[5] 出来合いの優れたサブルーチンが手に入るし、コードの最適化に心を砕かなくても計算機まかせのブルートフォースでなんとか欲しい結果が出力される、われわれのような日曜大工ならぬ日曜プログラマーにとっては本当にありがたい時代である。ここでは単一分子磁石となることで知られている車輪型の鉄７核錯体を解析した例を紹介しよう[6]。
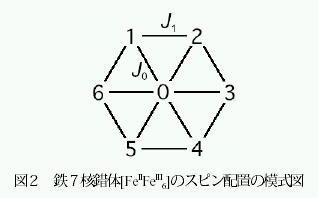　　この錯体は車輪のハブの位置にFe3+ (S = 5 / 2)をもち、リムに位置する六つのFe2+ (S = 2) とスポークを通して相互作用している分子構造（図２）で、スポーク部分の強い強磁性的相互作用のためS =29 / 2 という大きな基底スピンをもつ物質である。基底状態に限れば30 階の行列の対角化なので容易に解けるのだが、全てのスピン状態を考慮すると行列のランクは93750 階となりなかなか大変である。これでは何の工夫もしなければ行列要素を全部メモリーに格納するだけで65 GB にもなってしまう。仕方がないので今回は異方性は脇に置いておいて20 K 以上の高温側のデータだけをブロック対角化で解析することにした。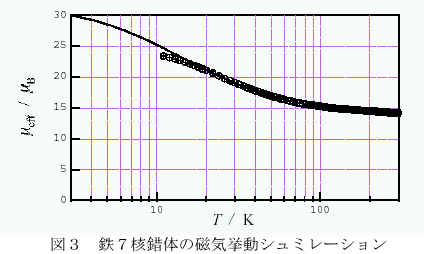

　　実は小さな行列（500 階程度まで）の計算ではスパコンよりパソコンの方が早いことが知られているのだが[7]、さすがにこのサイズになるとベクトル型のスパコンの方が圧倒的に早い。例に取った７核錯体では、あるスピンハミルトニアン・パラメーターのセットに対して磁化の温度依存性を求めるのは（つまり行列を１回対角化するのは）VPP5000 を使えば２時間程度の計算だが、Pentium4 (2.0GHz)1024MB RAM やAthlonMP (1.2GHz) 1024MB RAMでは2.5-3 日を要する。これだとパラメーターを変化させて最適化するのにパソコンを使うのはやや躊躇せざるをえない。パラメーター数３個のモデルを用いて最適化ループを20 回ほどまわした結果が図３であるが、磁気異方性の影響の少ない20 K 以上でよい一致が見てとれる。この計算は当初、定額制のメリットを生かして大阪大学CMC の演算サーバー上で行っていたのだがなかなか終わらず、結局VPP5000 上に移動してCPU time 100 時間程度を要した。（もっとも最適化ルーチンにダウンヒル・シンプレックス法[8-10] のリバースコミュニケーション版を使っているので効率が悪いという話もあるのだが…）
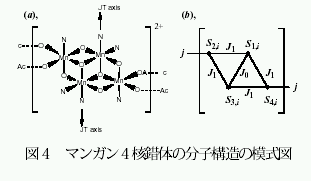　　もうひとつ、別の計算例としてマンガン４核錯体のHF-EPR スペクトルのシミュレーションを紹介しよう[11]。この錯体はMn2+ (S = 5/2) ２個、Mn3+ (S = 2) ２個からなる４核ユニットが酢酸架橋で結ばれた１次元鎖構造をとる（図４）。ユニット内には強い強磁性的相互作用がはたらいているため大きな基底スピンS = 9 をもち、隣接するユニット間にはたらく弱い反強磁性的相互作用により１次元イジング反強磁性体とみなすことができる。実際、磁化曲線や熱容量などの熱力学量は基底スピンだけ考慮したモデルでよく説明でき、2 K 程度の温度まで秩序化が起こらないという観測も１次元の特徴と符合している[12]。

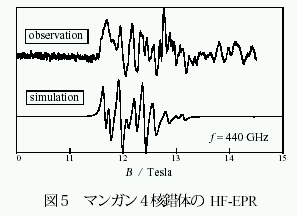　　ところが、電子常磁性共鳴を測定すると予想外に複雑なスペクトルが観測されるのである（図５）。これは隣接する４核ユニットとの相互作用のために、基底スピンS = 9 が巨大なひとつのスピンとして運動するという、通常の単一分子磁石でよく見られるシナリオが崩れて、肉離れした個々の成分スピンのキャラクターが見えてきているためである。
　　そこでシミュレーションに当たっては全てのマ
ンガンイオンのスピンを取り込んだモデルが要求さ
れる。とはいえ、全てのスピン状態を取り入れるとなるとユニット内だけで900 状態、隣接ユニット
との相互作用を考慮するためにゴーストスピンをくっつけると32400 状態と、４パラメーターモデル
の解析はおおごとになってしまう。MS = -9, -8, -7 の部分空間（540 状態）に問題を限定することによって、なんとかシミュレーションを試みたのが図５の下段である。良く合っているとはとても言えないが、熱力学量から求めたパラメーターとの整合性はほぼ満たされており、ある程度は満足できる結果を得ることができた。
　　この小文では、化学系の実験屋がどんな計算機の使い方をしているのか報告してきたが、量子化学計算に関しては全く触れることができなかった。分子構造の最適化が収束するまで数ヶ月間流しっぱなしというようなジョブの実行に当たって、定額制が大変ありがたかったという点だけ付け加えさせていただきたい。最後に、７核系の解析にあたり相談に乗っていただいた大阪大学CMC の菊池誠教授、プログラムがつまずく度に的確な助言をいただいたシステム運用管理掛の吉川勝氏に感謝いたします。

参考文献

  1. 武田啓司, 阿波賀邦夫, 固体物理, Vol.34, No.1, Pages 27-35 (1999);
    宮下精二, 日本物理学会誌, Vol.53, No.4, Pages 259- (1998).
  2. 中野元裕, 化学と工業, Vol.53, No.6, Page 704 (2000);
    M. Nakano, The News of Engineering Osaka University, Vol.13, Page 2 (2001).
  3. M. Eden and M. H. Levitt, Journal of Magnetic Resonance, Vol.132, Pages 220-239 (1998).
    <http://www.soton.ac.uk/~mhl/research/software/Orientations/>
  4. W. Gautschi, ACM Transactions on Mathematical Software, Vol.20, No.1, Pages 21-62 (1994).
    <http://www.netlib.org/toms/726>
  5. E. Anderson, Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling,
    A. McKenney, and D. Sorensen, "LAPACK Users' Guide, 3rd ed.", (Philadelphia: Society for Industrial & Applied
    Mathematics, 2000). <http://www.netlib.org/lapack/>
  6. H. Oshio, N. Hoshino, and T. Ito, International Symposium on Cooperative Phenomena of Assembled Metal Complexes,
    O-04 (Osaka, 2001).
  7. 「スーパーコンピュータの能力と有効活用」, OKAZAKI, No.3 (April, 2001).
    <http://www.orion.ac.jp/data/main_html/oshirase/syutupan/okazaki_2001_04/okazaki_2001_04.html>
  8. J. A. Nelder and R. Mead, Computer Journal, Vol.7, Pages 308-313 (1965).
  9. J. M. Parkinson and D. Hutchinson, in "Numerical Methods for Non-linear Optimization", Pages 115-135, Ed. by
    F. A. Lootsma (London: Academic Press, 1972).
  10. W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, "Numerical Recipes", (Cambridge: Cambridge
    University Press, 1986).
  11. M. Nakano, J. Yoo, D. N. Hendrickson, J. Krzystek, L.-C. Brunel, and G. Christou, Third Asia-Pacific EPR/ESR
    Symposium (APES'01), 2P52 (Kobe, 2001).
  12. A. Bhattacharjee, Y. Miyazaki, M. Nakano, J. Yoo, G. Christou, D. N. Hendrickson, and M. Sorai, Polyhedron, Vol.20,
    No.11-14, Pages 1607-1613 (2001).