格子QCDの数値シミュレーションによる
素粒子の強い相互作用の研究
中村純（広島大学情報メディア教育研究センター)
大規模数値計算によって大きな進展をとげている格子QCD シミュレーションについて、その基礎科学における位置付け、概要と現時点での限界を紹介する。これは、阪大核物理研究センターの全国共同利用プロジェクトの一環として、スーパーコンピュータSX-5を利用して我々のグループが進めている研究の紹介である。
１．素粒子の標準理論
ギリシャの哲学者、古代中国の賢人の時代より、我々の世界を構成する基本要素は何であるか、そこにはどのような法則が働くのかという問いは、人間の知的好奇心を刺激し、自然科学を発展させる大きな原動力であった。ボルツマン等の葛藤を経て[1]、現在、物質の基本要素としての原子の存在は疑いのないものとなっている。原子は、中心の原子核とその周りを回る電子から成る。原子核は、強く結びついた陽子と中性子から出来ている。電子と原子核の間に働く力は、我々の日常生活でも重要な役割を果たす電磁的な力であり、原子核の中のミクロな世界では強い相互作用と呼ばれる力が支配的である。また、ベータ崩壊などでは弱い相互作用と呼ばれる力が働く。強い相互作用をする粒子はハドロンと呼ばれ、非常に数多くあり、クォークとグルーオンというより基本的な素粒子からなると考えられている[2]。現在知られている基本的な力は、強い相互作用、電磁気力、弱い相互作用、それに重力である。重力の量子論は未だ完成していないが、それ以外の３つの力は、相対論的量子力学である場の量子論で記述され、さらに基本粒子を表す場を時空の各点でゲージ変換と呼ばれる操作をしても理論が不変であるゲージ場の理論で記述されることが明らかになってきた。電磁的力と弱い相互作用のゲージ理論はワインバーグ・サラム理論として統一され、クォークとグルーオンの力学はQCD (Quantum Chromo-dynamics 量子色力学) として完成した。これらを素粒子の標準理論という。ワインバーグ・サラム理論を現在の実験に適用するときには、摂動論が有効である。しかし、陽子、中性子、中間子などのハドロンをクォークとグルーオンから作り上げている力学であるＱＣＤは、ハドロンのスケールでは非常に強くなり、摂動論が適用できない。そして、通常、クォークとグルーオンが観測されない閉じ込めなどのハドロン物理学の特徴は、非摂動的な機構であると考えられている。現在、ＱＣＤに基づいてハドロンの振る舞いを研究するもっとも強力な手法が数値シミュレーションである[4, 5]。
２．格子QCD
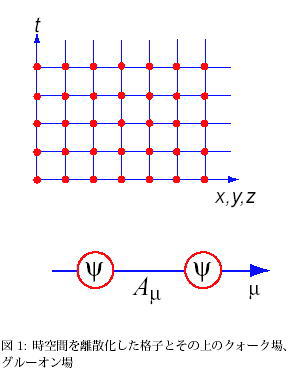
ファインマンは、古典的な経路だけではなく、いろいろな経路を積分する経路積分という形で量子力学が定1式化できることを示した。1974 年にウイルソンは[3]、標準理論でもっとも重要なゲージ対称性を保ったまま時空間を美しく離散化し、経路積分形式で定式化した格子ゲージ理論を作り上げた。クォーク場Ψ(x, y, z, t) は格子の各点上にあり、グルーオン場(Ax,Ay,Az, φ) = Aµはμ 方向のリンク（ボンド）の上にある。時空間の離散化により、無限に高い振動数は伝搬することができない。場の量子論は、量子化規則と、無限大の原因となる高い振動数の切断（カットオフ）の２つを与えて理論の定式化ができるが、ウイルソンの格子ゲージ理論は、経路積分で量子化規則、格子による高運動量の切断を与える量子化となっている。通常、場の量子論におけるカットオフの導入は、摂動論的な手法によって行われるが、格子ゲージ理論は、現在知られている唯一の摂動によらない量子化である。クォークとグルーオンの力学であるQCD もゲージ理論であり、格子上で定式化したものが格子QCD ある[6, 7]。格子QCDは、第一原理計算としてハドロン物理学の基礎を与えている。
３．格子QCDの数値シミュレーション
格子QCD の数値計算は、以下の2 つの部分が主となる：- グルーオン場をモンテカルロ手法で生成する(量子化のためのあらゆる経路を足しあげる経路積分)の部分
- そのグルーオン場の中で伝搬するクォークのプロパゲータに対応するフェルミオン行列の逆行列を解く部分
を、共役勾配法(CG法) 系列の解法で求める。格子QCD は、ハドロンに対する第一原理計算であるが、数値計算によるシミュレーションにおいては、以下のような問題がある：
(1) モンテカルロ計算に基づくため、有限のイテレーションによる統計誤差を持つ。(2)
格子間隔a が有限であるため、a → 0 の連続極限を取らなければならない。(3) ハドロン反応にもっとも寄与の大きいu, d クォークの質量は大変小さいが、その領域で線形方程式を解くことが困難であるため、より大きい質量で計算したものを外挿しなければならない。(4)
離散化された作用(アクション) は、連続理論の持つ重要な対称性であるカイラル対称性を満足していない。１格子のx, y, z, t 方向のサイズをNx,Ny,Nz,Nt とすると、フェルミオン行列のサイズはn ≡ 3×4×Nx ×Ny ×Nz ×Nt として、n × n となる。ここで3 はカラー自由度の数、4 はクォークと反クォークのスピンの上向き、下向きに相当する。NxNyNzNt = 324のサイズの格子では、約107 × 107 のサイズの行列になる。
４．格子QCD によるハドロン物理学の新しい流れ
近年、計算機の高速化、アルゴリズムと理論の発展により、これらの制限は大きく改良され、定量的な計算が可能となってきた。一方、欧州のCERN-SPS、米国のBNL-RHIC、国内のSpring-8、等で非常に精度の高い実験が蓄積され、高密度状態の実現を目指すドイツGSI、これまでにない高いビーム強度を目指す日本のJParc など特色をもった実験が計画されている。このような状況で、格子QCD のシミュレーションは第一原理計算として信頼度の高い情報、新しい情報を与えることが期待されている。以下、我々のグループのSX-5 による取組を簡単に紹介する。４．１ Unconventional ハドロン
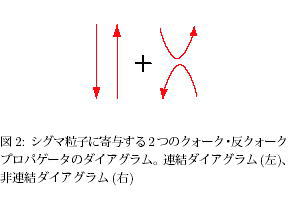
質量の計算(スペクトロスコピー) は、ハドロン物理学のもっとも基本的な量であるが、これまではクォーク模型でよく理解の進んでおり、実験的にも確立した粒子に対し、格子QCD がどこまで精度良く求められるかというアプローチが中心であった。日本の筑波グループは、conventional なハドロンに対しクォークの生成・消滅の効果を落す近似で数パーセントの精度で質量を求めることに成功した[10]。またKEK を中心とするグループは上記近似無しの大規模計算を進めている。この確立した手法で、実験的、現象論的に興味深いハドロンに対して今後計算を進めていくことが出来る。近年、大阪大学核物理学研究センターのグループによって発見されたペンタクォーク状態など[9, 11, 12] の理解にも大きく貢献すると思われる。我々は、真空と同じ量子数を持つシグマ粒子について、SX-5 を使って計算を進めている[8]。この粒子は、クォーク模型では非常に重いことが予想されるが、実験的にはそれほど重くないところに存在している。その結果、クォーク模型では考量することの難しい、クォークの非連結ダイアグラムが軽いシグマ粒子を作りだしていることが示された。
４．２ 有限温度
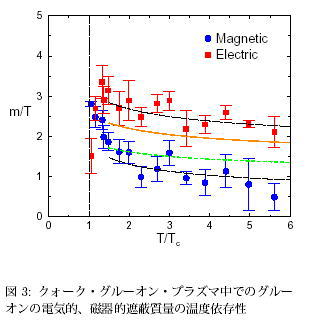
クォークとグルーオンは今まで単独の粒子としては発見されていない(閉じ込め)。しかし、超高温、超高密度では、この閉じ込めは破れることが予想されている。現在、米国BNL-RHIC で各国の実験グループがこの物質の新しい形態、クォーク・グルーオン・プラズマを発見するためにしのぎを削っている。我々は、有限温度でのハドロンの質量の計算を行い[13]、またクォーク・グルーオン・プラズマ中でのグルーオンの遮蔽質量を計算している[14, 15]。
４．３ 有限密度
超高密度のQCDは、高エネルギー重イオン反応、中性子星内部などで実現される可能性がある。特に、密度が高い時には、クォークがクーバー対を作るカラー超伝導が予言されており、非常に興味深い領域である。しかし、有限化学ポテンシャルにおいては、経路積分の測度が複素数になり、確率的操作であるモンテカルロ計算が非常に難しくなる。測度を絶対値と位相θ に分離すれば、exp(iθ) による符合問題となる[16]。化学ポテンシャルμ がゼロの時はもちろん通常の計算ができる。そこで我々は、有限温度で物理量を化学ポテンシャルμ = 0のまわりでデーラー展開して求める手法を提案し、計算を進めている[17]。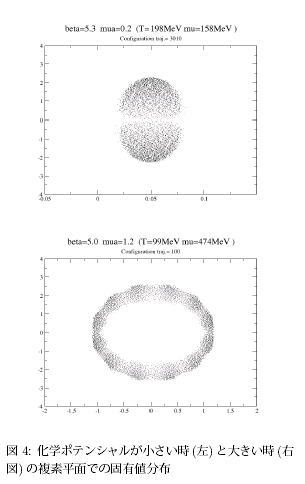
また、実際の計算の困難は、フェルミオン行列式の大きさにも強く依存する。ゼロに近い固有値があると、計算は困難になる。そこで、化学ポテンシャルを変えながら、固有値の分布を見ると、図のように固有値は巾を持ち始め、化学ポテンシャルが大きくなるにつれゼロに近づくが、更に大きくするとゼロのまわりに「穴」があいてしまうことが分かってきた。このことは、大きな化学ポテンシャルでは計算が可能であることを示唆している。
４．４ 散乱
格子QCD の数値シミュレーションでは、時間を虚時間に代えた定式化が通常使われるため、散乱を扱うことは難しいとこれまで思われてきた。しかし、有限ボックス中でのシミュレーションデータから散乱の基本情報を引き出す定式化がLüscher により提唱され、新しい可能性が開けてきた[18]。このLüscher 公式を使って、実験が難しい、あるいは十分に行われていないΛ-p、K-n、π-K などのチャンネルの計算を行う準備をしている[19]。これにより、J-PARC でのハイパー核の高精度のデータ、また核物理学研究センターの中野教授グループにより発見されたペンタクォークのK - n チャンネルへの結合等について、QCD に基づいた研究が進むことが期待される。５．まとめに代えて
筆者が２０年前に格子QCD の計算を始めたとき、ハドロンへの格子QCD の適用を始めて行ったパリジ先生に、我々はどこまで行けるのでしょうかと尋ねたことがある。先生は「クォーク模型も、ハドロンの質量という静的な量から始まり、磁気能率の計算、弾性散乱、パートン模型などによる多重発生の理解にまで進んできた。今は、質量以外どう計算したらいいか分からないが、格子QCD もクォーク模型と同じような計算が出来るようになるはずだ」とおっしゃった。いま確かにその時期に入り始めているのではないかと思われる。参考文献
[1] D. リンドリー,「ボルツマンの原子―理論物理学の夜明け」、青土社; ISBN: 4791760166
[2] 南部陽一郎、「クォーク―素粒子物理はどこまで進んできたか」講談社ブルーバックス, ISBN:4062572052 (第２版)
[3] K. Wilson, Phys. Rev. D10, 2445 (1974).
[4] 岩崎洋一、物理学最前線11『格子ゲージ理論』（共立出版）
[5] S. Choe, 中村純, 野中千穂, 室谷心, Lattice QCD Tool Kit in Fortran90, 素粒子論研究108 巻1 号（2003 年10 月号） page 1-43.
[6] I. Montvay, G. Munster, Quantum Fields on a Lattice (Cambridge Monographs on Mathematical Physics), Cambridge Univ. Press.
[7] J. Smit, Introduction to Quantum Fields on a Lattice, Cambridge Lecture Notes in Physics, Cambridge Univ. Press.
[8] SCALAR Collaboration: T. Kunihiro, S. Muroya, A. Nakamura, C. Nonaka, M. Sekiguchi and H. Wada, “Scalar Mesons in Lattice QCD”, hep-ph/0310312,
[9] LEPS Collaboration: T. Nakano, et al, Phys. Rev. Lett. 91 (2003) 012002, “Evidence for Narrow S=+1 Baryon Resonance in Photoproduction from Neutron”,
[10] CP-PACS Collaboration: S. Aoki et al., Phys. Rev. Lett. 84 (2000) 238-241, “Quenched Light Hadron Spectrum”.
[11] S. Sasaki, hep-lat/0310014, “Lattice study of exotic S=+1 baryon”
[12] F.Csikor, Z. Fodor, S.D. Katz and T.G. Kovacs, JHEP 0311 (2003) 070, “Pentaquark hadrons from lattice QCD”
[13] QCD-TARO Collaboration, Phys. Rev. D63 (2001) 054501, “MESON CORRELATORS IN FINITE TEMPERATURE LATTICE QCD”
[14] A. Nakamura, I. Pushkina, T. Saito and S. Sakai, Phys.Lett. B549 (2002) 133-138, “Screening of hot gluon”.
[15] A. Nakamura, T. Saito and S. Sakai, Phys. Rev. D69 (2004) 014506, “Lattice Calculation of Gluon Screening Masses”.
[16] S. Muroya, A. Nakamura, C. Nonaka and T. Takaishi, Prog. Theor. Phys. 110, (2003) pp.615- 668, “Lattice QCD at Finite Density An introductory review”.
[17] QCD-TARO Collaboration, Phys. Rev. D65 054501,2002, “Responses of hadrons to chemical potential at .nite temperature”.
[18] M. L¨uscher, Commun. Math. Phys. 105 (1986) 153; Nucl. Phys. B354 ( 1991), 531; B364 (1991), 237.
[19] L-cube collaboration: S. Muroya, J. Nagata and A. Nakamura, to appear in Proceedings of Lattice Fiedls Theory 2003.