大規模計算科学研究部門
Large-Scale Computational Science Division
１． 部門スタッフ
教授 菊池誠略歴: 1986 年3 月東北大学大学院理学研究科物理学専攻後期課程修了、1987 年2 月大阪大学理学部物理学科助手、1993 年8 月同助教授（改組により、現在、大阪大学大学院理学研究科）、2000年4 月より、大阪大学サイバーメディアセンター大規模計算科学部門教授。日本物理学会、日本応用数理学会各会員。理学博士。
助教授 時田恵一郎
略歴: 1994 年3 月東京大学大学院理学研究科相関理化学専攻博士課程修了、1994 年4 月大阪大学理学部物理学科助手、2000 年4 月より、大阪大学サイバーメディアセンター大規模計算科学部門助教授。日本物理学会、アメリカ物理学会、数理生物学懇談会各会員。理学博士。
２． 教育および教育支援業績
本年度は以下の学内の講義を担当した(1) 共通教育・専門基礎科目
力学要論（工学部、時田）
(2) 共通教育・情報処理教育科目
計算機シミュレーション入門（菊池）
(3) 共通教育・主題別科目
科学と人間（「科学とニセ科学」の回を担当、菊池）
(4) 共通教育・基礎セミナー
楽器を作ろう・・・音の科学入門（菊池、分担）
(5) 理学部専門科目
物理数学2 （物理学科、菊池）
物理数学3 （物理学科、時田）
物理学輪講・宇宙地球科学輪講（物理学科、時田、分担）
物理学特別研究（物理学科、菊池・時田、分担）
(6) 大学院理学研究科科目
物性理論特論II （物理学専攻、菊池）
非線形物理学 （物理学専攻、菊池）
多体問題セミナーII （物理学専攻、菊池・時田）
(7) 大学院生命機能研究科科目
基礎数学2 （菊池、分担）
コンピューター科学演習（時田）
３． 研究概要
本部門の研究分野をひとことでまとめると学際計算物理学である。統計力学や非線形動力学の理論を基礎とし、計算機シミュレーションなどの計算物理学的手法を用いて、物理学と生物学や工学との学際領域の研究に取り組んでいる。現在の主な研究テーマはタンパク質の折り畳みとデザイン、分子モーターの運動機構解明、大規模生態系の進化と安定性、高速道路交通流、砂丘のダイナミクスなどである。また、計算科学の分野では計算手法の開発も重要な課題である。我々の部門では、その中でも特にモンテカルロシミュレーションの拡張（拡張アンサンブル法）について、精力的に研究を行っている。さらに、新しい自由な計算環境構築を目指して、PC クラスターの運用実験も進めており、サイバーメディアセンターのBiogrid プロジェクトと連携して、Grid 環境下での計算手法についても研究している。４． 研究成果
４．１ タンパク質の機能とゆらぎ
タンパク質の計算物理学的研究としては、第一原理的に天然構造を予測するという大目標があり、多くの研究者によって全原子模型に基づく分子動力学計算が行なわれている。一方、我々のグループの興味は天然構造予測ではなく、折れたたみ過程そのもののメカニズムや機能を果たすための大変形のメカニズムを明らかにすることにある。そのために我々は、タンパク質の構造空間で見た自由エネルギー景観の特徴を調べている。研究手法も全原子計算ではなく、格子模型やバネ・ビーズ模型など粗視化されたモデルに基づく計算機シミュレーションである。なお、格子模型の熱平衡状態計算については、我々が統計数理研究所・伊庭幸人助教授と協力して開発したMulti-Self-Overlap Ensemble(MSOE) Monte Carlo 法が現時点で世界最強の計算手法であり、この手法の利点を生かした計算を行なっている。4.1.1 分子モーターおよび関連タンパクの自由エネルギー構造
我々はこれまで、モータータンパク質であるキネシンの熱平衡ゆらぎを調べてきたが、本年度はさらにキネシンのレールタンパクである微小管についても、熱平衡での構造揺らぎ解析をおこなった。計算に用いたモデルは、これまでと同様にX 線結晶解析をもとにした格子模型に郷モデルと呼ばれる天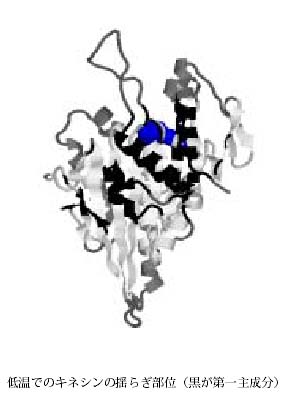
然構造を必ず再現する人工的な相互作用を与えたものである。計算手法としてはMSOE
法を用いた。我々が行なったキネシンの計算は熱平衡計算としては残基数で過去最大のものだったが、今回それよりさらに長い微小管タンパクの熱平衡計算に成功した。構造揺らぎについては、熱平衡での相関関数に主成分分析を適用して解析した。結果として、低温ではキネシンと微小管のいずれも相互結合部位に大きな構造揺らぎが局在していることを見出した。この事実は、モーターとしての機能発現には両者の構造揺らぎ、言い換えると両タンパクの共同的な“部分unfold” と“refold” を利用した結合解離制御が重要な役割を果たしていることを意味する。すなわち、レールタンパクは単なる静的なレールとして存在するのではなく、その構造揺らぎを通してキネシンの運動に積極的に関わっているのである。結合解離制御が熱揺らぎを利用して実現されている点は、「柔らかい機械」としての分子モーターならではのメカニズムである。
他に関連分子モーター関連タンパクとしてRAS の構造ゆらぎについても計算を行った。
4.1.2 タンパク質の凝集
プリオン病では脳内にタンパクが凝集したアミロイド繊維ができることが知られている。しかしながら、タンパク質凝集を熱力学の見地からきちんと扱った研究はほとんどない。ヘモグロビンのように複数のタンパクが凝集して四次構造を作るものがあることからも明らかな通り、凝集とは複数のタンパクが全体としてfoldする現象である。したがって、凝集の研究にはfolding現象と同じ手法が応用できる。ただし、たとえば二個のタンパク質だけからなる系は熱力学的に異常な系であって、一般には状態が正しく定義されない。そのため、計算機シミュレーションで凝集を調べるにしても、やみくもに計算するだけでは本質的な部分で曖昧さが残る。そこで我々は、この困難を克服して、きちんと状態を定義した上でタンパク質凝集を議論することを試みた。ターゲットとして、凝集の最小単位である二個のタンパク質の問題を取り上げた。ポイントはタンパクを閉じ込める「箱」を定義することである。熱力学的な状態は箱の体積を指定することによってきちんと定義でき、さらに自由エネルギーの体積依存性から、凝集状態の安定性が議論できる。具体的な計算は格子タンパク質モデルとMSOE 法を用いて行なった。結果として、ある温度を境に凝集体が不安定から準安定に変わるある種の相転移を見出した。また、体積の逆数を濃度とみなすと、濃度に対する凝集体の安定性の変化についても議論できる。計算結果は、タンパク質の濃度が高ければ凝集体が熱力学的安定状態になりうることを示している。これは、タンパク質濃度が凝集開始に本質的に重要であることを示唆する。
４．２ 大規模生態系モデルの数理
数理生物学を中心とする様々な分野で研究されている進化力学系（レプリケータ方程式系）の数理的研究を行っている。特に、関係している種数が多く、種間相互作用が複雑で多様な「大自由度ランダム群集モデルの研究に力を入れている。大自由度ランダム群集モデルは、生態学だけでなく、多数の戦略が関わる巨大な社会・ゲーム力学系や、多数の遺伝子が関わる遺伝子発現のネットワーク、細胞内での巨大な代謝反応ネットワークのモデルなどとも数学的に等価であることが知られており、大規模で複雑な生物ネットワーク一般の振る舞いを解明するための重要なツールであると考えている。より広い数理科学的な視点からは、カオスやヘテロクリニックサイクルなどの非常に豊富な力学的振る舞いを生み出す最も簡単な非線形力学系の一つとして興味深い。これまでに、相互作用行列の要素間の相関と、系の巨視的な振る舞いの関係について調べてきた。昨年度までは、特に、相互作用行列が、ランダム非対称行列やランダム反対称行列の場合に注目して、種数の時間変動などの、系の巨視的な振る舞いを分類してきた。今年度はランダム対称行列の場合について調べた。これは、昨年度までに調べた、群集アセンブリモデル(Tokita &Yasutomi, Theor. Popl. Biol. vol.63, 2003) が進化してできあがった群集のモデルになっている。このモデルに関しては、相互作用の対称性から、統計力学的な取り扱いが可能で、個体数分布、種の豊富さの分布など、これまでに野外研究で蓄積されてきた巨視的なパターンを、複雑な相互作用をもつ基礎的かつ微視的な進化ダイナミクスと理論的に結びつけることができた。これについては現在論文を投稿中である。
４．３ 高速道路交通流の数理と実験
高速道路上で見られる交通流のふるまいは、一次元非線形動力学の問題として一部の物理学者の注意をひいている。我々は、この問題に対し、数理モデルの構築と計算機シミュレーションを行っている。また、シミュレーションの正当性は結局観測事実との整合性でしか言えないことから、現実の高速道路交通流で得られる観測データの解析にも力をいれており、計算と観測（データ処理）の2 方向から交通流の問題にとりくんでいる。本年度の特筆すべき成果は、数理モデルから得られる結果を検証するために、実物の車両を使った実験を行なったことである。交通工学では、渋滞はボトルネック上流でのみ生じるというのが“常識” だった。一方、これまでに多くの数理モデルが渋滞流と自由流の間で明確な相転移があることを予言してきたが、転移のコントロール・パラメータが“全系の車両密度”であったために現実の高速道路交通流では相転移を実証できなかった。そこで、実際に半径37m の円周路に22 台の車両を走らせる実験を行なった結果、車両密度を固定した状況下ではボトルネックがなくても渋滞が自然に発生することを実証できた。なお、この実験の模様はフジテレビ系の「交通バラエティ」でも紹介された。
また、東名高速道路や伊勢道など高速道路上の数十ヶ所で取得された各一年分の流量データについて、Detrended Fluctuation Analysis と呼ばれる方法を用いて再検討を試みたところ、昨年度は一部の周波数領域でしか見いだせなかった流量ゆらぎの1/f ノイズが、実は数十分から数十日にわたる広い時間スケールにわたって一貫して存在することを見いだした。これはかなり意外な結果と言わざるをえない。特に長時間スケールでのゆらぎについてはメカニズムが不明である。
４．４ バルハン砂丘群のダイナミクス
バルハン（三日月型砂丘）は、風が一方向に吹きかつ砂の量があまり多くない砂漠で観測されるもので、地球上だけでなく火星でも発見されている。これまでは、バルハンが単独でも安定に存在すると考えられていたことや、変化の時間スケールが極めて長いことなどの理由から、その集団運動はほとんど注目されてこなかった。特に、衝突現象のタイムスケールは数年から数百年にわたるので、全過程を観測できず、衝突ダイナミクスについての系統的な研究は行われていなかった。しかし、2 年前に水槽下でバルハン砂丘形成実験が成功し、砂丘を実験室内で取り扱えるようになったことから、砂丘の動力学研究は今まさに巨大な転換点を迎えている。これを受けて、我々は砂丘の動力学の本質を捉えた「砂丘のミニマルモデル」を提案した。このモデルは素過程として飛砂と雪崩の効果だけを単純化して取り入れた結合写像型のもので、流体の複雑な振る舞いなどは無視しているにもかかわらず、計算機シミュレーションを行った結果、実験で観測されたバルハンの生成や衝突・合体・分裂などを再現できた。このモデルの成功は、砂丘の形態形成にとって本質的に不可欠なプロセスは飛砂と雪崩のふたつだけであることを示している。
このモデルを用いて、我々は2 砂丘の衝突には、衝突後に合体する場合と分裂する場合があることを見いだした。合体・分裂のタイプは2 砂丘の質量比と衝突位置によって分類できる。さらに、砂床からのバルハン形成シミュレーションにも成功した。これにより、原理的には砂漠全体のシミュレーションも研究の視野にはいってきたと言える。
また、数理的研究と並行して、大阪大学理学研究科宇宙地球専攻・遠藤徳孝助手のグループと共同でバルハン衝突現象の系統的な実験を行った。遠藤グループは一方向水流のもとでバルハン形成実験に成功している世界で唯一の実験グループである。実験の結果、シミュレーションが衝突過程の細部までよく再現していることが確かめられた。
４．５ モンテカルロ・シミュレーションの新技法の開発
温度一定のアンサンブルを構成するために、従来はメトロポリス流のモンテカルロ・シミュレーションが使われてきた。しかし、最近になってカノニカル（温度一定）ではないアンサンブルへの興味が高まり、特に、シミュレーションで人為的なアンサンブルを構成した後、得られたアンサンブルから温度一定アンサンブルを再構築するという、いわゆる“拡張アンサンブル”の方法に注目が集まっている。もともとは物理学の分野で発展したアイデアだが、現在その適用範囲は情報処理や統計学の広い分野にわたっている。従来の“温度を与えて手を放す”シミュレーションから、“積極的にコントロールする（しかし、最終結果は正しい温度一定アンサンブルになる）”シミュレーションへの流れは、今後も続くはずである。我々のグループは“拡張アンサンブル”の先導的な研究グループのひとつであり、特にタンバクのモデルをターゲットとした拡張アンサンブル法に重点を置いて研究を進めてきた。本年度は、昨年度に引き続いて連続自由度のモデルに対して、MSOE を拡張する研究を行った。元のMSOE法は極めて強力な計算手法ではあるが、「アミノ酸残基同士の重なり」が整数値で表わされるという格子モデルの特性をフルに利用していたため、連続自由度のモデルにそのままの形では適用できない。そこで、「緩和を遅くする制約条件を緩める」というMSOE の精神を引きつぎ、二体間相互作用を引力部分と斥力部分に人為的に分割した上で、斥力部分を弱めることによって緩和を速くするという手法を提案し、計算を試みた。これまでにαへリックス三本で構成されるタンパクを題材とした予備計算を行い、ある程度の有効性はすでに確認できている。この手法は斥力に起因するゆらぎと引力に起因するゆらぎを完全に分離して扱えることから、単に計算の効率化だけではなく、タンパクの機能を調べる際の解析手段としても有望と考えている。
４．６ 密度行列繰り込み群
密度行列繰り込み群は、多自由度量子系の自由度を系統的に消去して、少ない計算量でなおかつできるだけ正確に量子状態を求めるための方法である。我々のグループでは、この方法の基礎的研究を行うとともに、低次元の磁性物質に適用している。本年度は二次元チェッカーボード格子上の反強磁性XXZ モデルに対して「テンソル積状態」を用いた定式化を行った。４．７ ＰＣクラスタの構築（待兼山計畫）
我々は、自由な計算環境構築を目指して、主にシミュレーションを用途とするPC クラスタを自作・運用している。本年度は新たに14 台のDual Xeon 機を導入し、主として分子モーターの研究に利用している。また、サイバーメディアセンターが中心となって展開しているBiogrid プロジェクトに参画し、Grid 基盤グループのメンバーとしてGrid 環境下での計算技法に関する基礎的研究にも取り組みつつある。４．８ 研究協力
学内・学外の多くの研究者と積極的に研究協力を行うことにより、研究の活性化を計っている。また、博士研究員として高城史子氏、理学研究科物理学専攻博士課程学生として剣崎博生・勝木厚成の2 名が研究に参加している。５． 社会貢献に関する業績
５．１ 教育面における社会貢献
5.1.1 学外活動
（１）財団法人大阪都市協会が運営するlog osaka web magazine で、一般向け物理学講座「かわいい物理音」をストリーミング配信中(URL:http://www.logosaka.jp/broadcasts/workroom/workroom_index4.html)（菊池）5.1.2 他大学非常勤講師
（１）京都女子大学「文化としての科学2」（分担, 菊池）５．２ 研究面における社会貢献
5.2.1 他大学セミナー講師
（１）時田恵一郎, “ランダム群集モデルにおける多種共存と個体数の豊富さのパターン” （2003 年5月, 東北大学大学院情報科学研究科）（２）時田恵一郎, “ランダム群集モデルにおける多種共存と個体数の豊富さのパターン” （2003 年5月, 京都大学生態研センター）
（３）時田恵一郎, “複雑な生物ネットワークにおける安定性と多様性の維持メカニズム”（2003 年8 月,京都大学化学研究所バイオインフォマティクス研究センター）
（４）Kei Tokita, “Statistical mechanics of species abundancepatterns”, (Nov. 2003, Harvard University,Program for Evolutionary Dynamics (PED))
（５）菊池誠, “拡張アンサンブルとその周辺” （2004年2 月, 龍谷大学理工学部）
５．３ 学会活動
5.3.1 国内学会における活動
（１）日本物理学会WWW 小委員会委員（菊池）（２）基礎物理学研究所計算機委員会所外委員（菊池）
（３）日本数理生物学会運営委員（時田）
5.3.2 論文誌編集
（１）「物性研究」各地編集委員（菊池）5.3.3 研究集会世話人
（１）基研研究会「ソフトマターの物理学2003 －普遍性と多様性」2003 年7 月30 日～8 月１日, 京都大学基礎物理学研究所（高城）（２）JST 異分野研究者交流促進事業フォーラム「無駄の効用－揺らぎと遊び」2004 年1 月12 日～15 日,加賀市・ホテルアローレ（菊池）
５．４ プロジェクト活動
（１）平成14(2002) 年度～ 科学技術振興機構・戦略的創造研究推進事業「ゆらぎと生体システムのやわらかさをモデルとするソフトナノマシン」（菊池:分担, 研究代表者: 柳田敏雄（大阪大学生命機能研究科））（２）平成15(2003) 年度～平成17(2005) 年度科学研究費補助金基盤研究(C)(2)「交通流の動的性質－実測データ解析とシミュレーション」（菊池: 分担,研究代表者: 只木進一（佐賀大学学術情報処理センター））
（３）平成14(2002) 年度～平成15(2003) 年度科学研究費補助金若手研究(B)「生物多様性の維持機構に関する統計力学的・計算物理学的研究」（研究代表者: 時田）
６． 2003 年度研究発表論文一覧
６．１ 著書
（１）大貫惇睦編著『物理学への誘い（改訂版）』（菊池, 分担:「力学」を分担執筆および「熱とエネルギー」を執筆）大阪大学出版会、2003 年（２）『生態学辞典』（時田, 分担:「ランダム群集モデル」担当）, 共立出版, 2003 年
６．２ 解説記事
（１）菊池誠, “すべては熱になる: 熱力学第二法則”,細胞工学, 23 (2004) No.3. , 371-376（２）菊池誠, “確率小話”, 細胞工学, 23 (2004) No.4,473-478
６．３ 原著論文
（１）F. Takagi, N. Koga, and S. Takada, “How protein thermodynamics and folding mechanisms are altered by the chaperonin cage: Molecular simulations”Proc. Natl. Acas. Sci., 100 (2003) 11367-11372.（２）N. Maeshima,“Tensor product state formulation for the spin 1/2 antiferromagnetic XXZ model on the checkerboard lattice”, J. Phys. Soc. Jpn., 73 (2004) 60.
６．４ 国際会議会議録
（１）S. Tadaki, M. Kikuchi, K. Nishinari, Y. Sugiyama and S. Yukawa, “Congestion Induced by Bottlenecks in Two-lane Optimal Velocity Traffic Flow Model” , Traffic and Granular Flow ’01 (Springer, 2003) .（２）S. Yukawa,M. Kikuchi, A. Nakayama, K. Nishinari, Y. Sugiyama and S. Tadaki,“Observational Aspects of Japanese Highway Traffic”, Traffic and Granular Flow ’01 (Springer, 2003) .
（３）M. Kikuchi, A. Nakayama, K. Nishinari, Y. Sugiyama, S. Tadaki and S. Yukawa, “Long-Term Traffic Data from Japanese Expressway”, Traffic and Granular Flow ’01 (Springer, 2003) .
６．５ 口頭発表（招待講演・一般講演）
（１）時田恵一郎, “大規模進化力学系における多様性維持のメカニズム”, DNA コンピューティング研究会（2003 年4 月, 早稲田大学教育学部）（２）時田恵一郎, “ランダム群集モデルにおける多種共存解と種の豊富さのパターン”, 日本進化学会2003 年福岡大会（2003 年8 月, 九州大学）
（３）Y. Sugiyama, M. Kikuchi, A. Nakayama, A. Nishinari, K. Shibata, S. Tadaki and S. Yukawa,“Traffic Flow as Physics of Many-Body System”, 10th IFAC Symposium on Control in Transportation Systems (Aug. 2003, Seikei Univ, Tokyo)
（４）M. Kikuchi, Y. Sugiyama, S. Tadaki and S. Yukawa, “Formation of Synchronized Flow at the Upper Stream of Bottleneck in Optimal Velocity Model”, 10th IFAC Symposium on Control in Transportation Systems (Aug. 2003, Seikei Univ, Tokyo)
（５）時田恵一郎, “ランダム群集モデルにおける種の豊富さのパターンの統計力学”, 第13 回数理生物学シンポジウム（2003 年9 月, 奈良女子大学）
（６）前島展也, 奥西巧一, 坂井徹、岡本清美,“フラストレートしたボンド交替鎖の磁場中相図”, 日本物理学会2003 年秋期大会（2003 年9 月, 岡山大学）
（７）勝木厚成， 遠藤徳孝，西森拓, “砂丘群のダイナミクス(open boundary)”, 日本物理学会2003 年秋期大会（2003 年9 月, 岡山大学）
（８）検崎博生，菊池誠, “格子モデルによる，モータータンパク質の自由エネルギー構造”, 日本生物物理学会・ポスターセレクションシンポジウム講演（2003 年9 月, 新潟コンベンションセンター）
（９）M. Kikuchi, A. Nakayama, K. Nishinari, A. Shibata, Y. Sugiyama, S. Tadaki and S. Yukawa,“Fluctuationin Expressway Traffic Flow”, International workshop on Traffic and Granular Flow ’03 (Oct. 2003,TU Delft, Netherland)
（１０）N. Maeshima, “Magnetization Process of the Frustrated Bond-Alternating Chain”, Third Open Symposium on Research Project, Grant-in-Aid for Scientific Research on Priority Areas: “Field-Induced New Quantum Phenomena in Magnetic Systems” （2003 年11 月, 国際高等研究所）
（１１）前島展也, 奥西巧一, 岡本清美、坂井徹, “フラストレートしたS=1/2 ボンド交替鎖の磁場誘起相転移”, 物性研短期研究会「フラストレーションが創る新しい物性」（2003 年12 月, 東京大学物性研究所）
（１２）勝木厚成，“バルハン砂丘の衝突、合体、分裂”,「動力学視点からの地形進化の研究」研究会（2003年12 月, 京都大学基礎物理学研究所）
（１３）勝木厚成, “砂丘群の相互作用”, 「動力学視点からの地形進化の研究」研究会（2003 年12 月, 京都大学基礎物理学研究所）
（１４）杉山雄規, 福井稔, 菊池誠，長谷部勝也, 中山章宏, 西成括祐, 及川浩和, 只木進一, 湯川諭, 吉田立, “自然渋滞発生のサーキット実験”, 日本物理学会第59 回年会（2004 年3 月, 九州大学）
（１５）只木進一, 菊池誠，中山章宏, 西成括祐, 柴田章博, 杉山雄規, 湯川諭, “交通流時系列における特徴的時間スケール”, 日本物理学会第59 回年会（2004 年3 月, 九州大学）
（１６）下山紘充， 菊池誠, “拡張アンサンブル法を用いた，タンパク質粗視化モデルの計算”, 日本物理学会第59 回年会（2004 年3 月, 九州大学）
（１７）中西良樹， 菊池誠, “2 つの格子たんぱく質間の相互作用がある系での自由エネルギーランドスケープ”, 日本物理学会第59 回年会（2004 年3 月,九州大学）
（１８）勝木厚成， 遠藤徳孝，西森拓, “バルハン砂丘の衝突過程”, 日本物理学会第59 回年会（2004 年3 月, 九州大学）
（１９）西森拓， 寺田昌弘, 勝木厚成, “砂丘群の相互依存ダイナミクスII”, 日本物理学会第59 回年会（2004 年3 月, 九州大学）
６．６ 修士論文
（１）下山紘充, 『拡張アンサンブルを用いた粗視化タンパク質の計算』（大学院理学研究科物理学専攻）（２）中西良樹, 『格子タンパク質の二量体の安定性』（大学院理学研究科物理学専攻）